Ôn Tập A – Z Về Hàm Số Mũ, Hàm Số Lôgarit Nhanh Chóng

Với kỳ thi THPT Quốc gia cận kề, việc nắm vững kiến thức về hàm số mũ và hàm số logarit là chìa khóa để đạt điểm cao trong môn Toán. Để giúp học sinh hệ thống kiến thức và luyện tập hiệu quả, Trường Việt Anh đã tổng hợp các lý thuyết quan trọng và bài tập mẫu. Hãy cùng ôn tập toàn diện để tự tin bước vào kỳ thi nhé!

1. Lý Thuyết Hàm Số Mũ và Hàm Số Logarit

a. Lý Thuyết Về Hàm Số Mũ

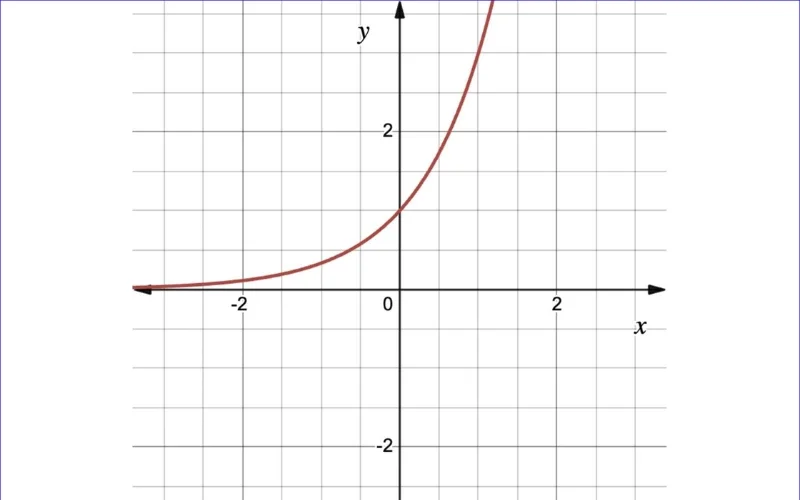
Hàm số mũ là hàm số có dạng y=axy = a^xy=ax với $a>0$ và a≠1a \neq 1a=1. Một ví dụ phổ biến của hàm số mũ là y=exy = e^xy=ex với cơ số $e$, thường gặp trong nhiều bài toán thực tế. Đồ thị của hàm số mũ thường có dạng đường cong đồng biến khi $a>1$, và nghịch biến khi $0<a<1$.

Ví dụ:

• y=10xy = 10^xy=10x: Cơ số là 10.
• y=exy = e^xy=ex: Cơ số là $e$ (hằng số Euler, xấp xỉ 2.718).

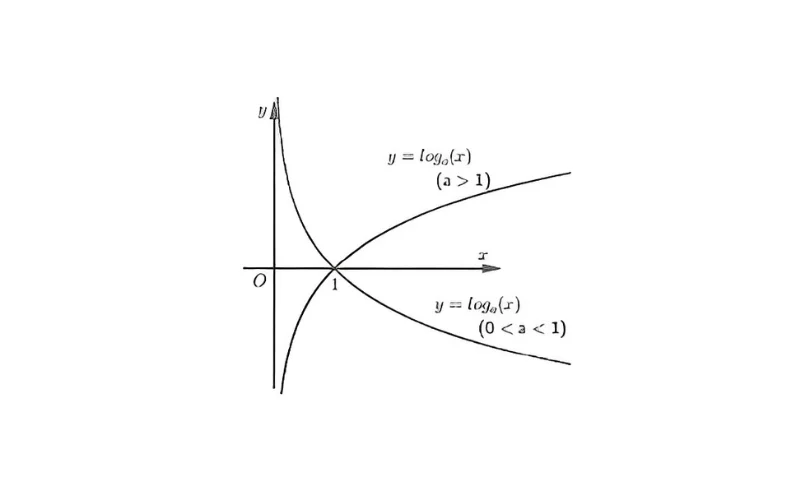
b. Lý Thuyết Về Hàm Số Logarit

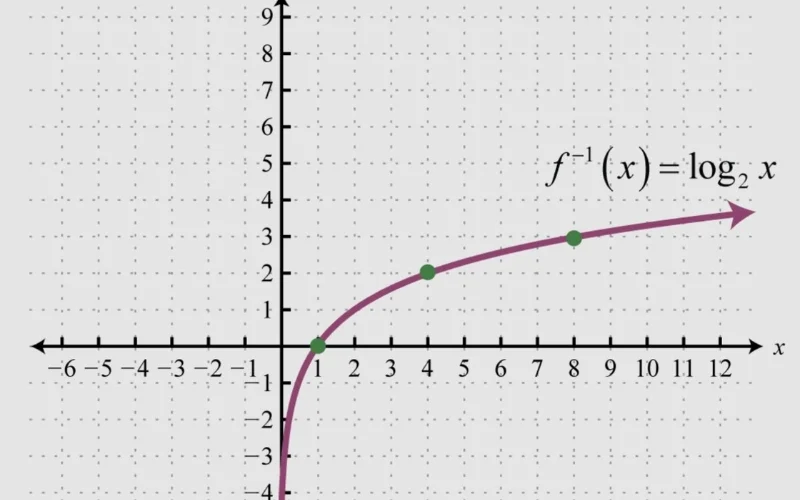
Hàm số logarit là hàm số ngược của hàm số mũ. Công thức cơ bản của hàm số logarit là y=log⁡axy = \log_a{x}y=loga​x, trong đó $a>0$ và a≠1a \neq 1a=1. Đồ thị của hàm số logarit thường đồng biến khi $a>1$, và nghịch biến khi $0<a<1$.

Ví dụ:

• y=log⁡10xy = \log_{10}{x}y=log10​x: Hàm logarit cơ số 10.
• $y=\ln x$: Hàm logarit tự nhiên cơ số $e$.

2. Tính Chất Của Hàm Số Mũ và Hàm Số Logarit

Để giải các bài toán liên quan đến hàm số mũ và logarit, việc nắm vững tính chất của chúng là điều cần thiết.

a. Tính Chất Của Hàm Số Mũ

1. Tập xác định: $D=(-\infty ,+\infty )$.
2. Đạo hàm:
   • (ex)′=ex(e^x)’ = e^x(ex)′=ex.
   • (ax)′=axln⁡a(a^x)’ = a^x \ln{a}(ax)′=axlna với $a>0$, a≠1a \neq 1a=1.
3. Chiều biến thiên:
   • Khi $a>1$, hàm số luôn đồng biến.
   • Khi $0<a<1$, hàm số nghịch biến.

b. Tính Chất Của Hàm Số Logarit

1. Tập xác định: $D=(0,+\infty )$.
2. Đạo hàm:
   • (log⁡ax)′=1xln⁡a(\log_a{x})’ = \frac{1}{x \ln{a}}(loga​x)′=xlna1​.
3. Chiều biến thiên:
   • Khi $a>1$, hàm số đồng biến.
   • Khi $0<a<1$, hàm số nghịch biến.

3. Khảo Sát và Vẽ Đồ Thị Hàm Số Mũ và Logarit

a. Khảo Sát Hàm Số Mũ

Để khảo sát và vẽ đồ thị của hàm số mũ y=axy = a^xy=ax, ta thực hiện các bước sau:

• Tập xác định: $D=\mathbb{R}$.
• Tập giá trị: $T=(0,+\infty )$.
• Chiều biến thiên: Hàm đồng biến nếu $a>1$, và nghịch biến nếu $0<a<1$.

b. Khảo Sát Hàm Số Logarit

Với hàm logarit y=log⁡axy = \log_a{x}y=loga​x, ta thực hiện các bước sau:

• Tập xác định: $D=(0,+\infty )$.
• Tập giá trị: $T=\mathbb{R}$.
• Chiều biến thiên: Hàm đồng biến khi $a>1$, và nghịch biến khi $0<a<1$.

4. Các Thủ Thuật Giải Bài Tập Về Hàm Số Mũ và Logarit

a. Tìm Tập Xác Định Của Hàm Số

Một trong những bước cơ bản khi làm bài tập về hàm số mũ và logarit là tìm tập xác định. Để tìm tập xác định của một hàm số mũ, ta chỉ cần xác định điều kiện để biểu thức trong hàm mũ có nghĩa.

Ví dụ:

• Với hàm số y=(x+3)2018y = (x+3)^{2018}y=(x+3)2018, tập xác định là $D=\mathbb{R}$ vì mọi giá trị của $x$ đều có nghĩa.

b. Ví Dụ Về Hàm Số Logarit

Với hàm logarit, tập xác định là các giá trị làm cho biểu thức trong dấu logarit dương. Ví dụ:

• Với y=log⁡(x2−4x+3)y = \log(x^2 – 4x + 3)y=log(x2−4x+3), điều kiện xác định là x2−4x+3>0x^2 – 4x + 3 > 0x2−4x+3>0, từ đó suy ra tập xác định $D=(-\infty ,1)\cup (3,+\infty )$.

5. Một Số Dạng Bài Tập Cơ Bản

a. Dạng 1: Tìm Hàm Số Từ Đồ Thị

Dạng bài này yêu cầu học sinh nhận biết đồ thị của hàm số mũ hoặc logarit và xác định hàm số tương ứng. Ví dụ: nếu đồ thị là một đường cong đồng biến, khả năng cao đó là đồ thị của một hàm số mũ.

b. Dạng 2: Tìm Mối Quan Hệ Giữa Các Cơ Số

Dạng bài này yêu cầu tìm mối quan hệ giữa các cơ số của hàm số mũ hoặc logarit dựa trên đồ thị. Học sinh cần chú ý đến tính chất đồng biến hoặc nghịch biến của đồ thị để xác định mối quan hệ giữa các cơ số.

c. Dạng 3: Tính Đạo Hàm Của Hàm Số

Dạng bài tính đạo hàm của hàm số mũ và logarit thường xuyên xuất hiện trong các kỳ thi. Công thức tính đạo hàm của hàm mũ và logarit đã được nêu ở phần trên.

d. Dạng 4: Tính Giới Hạn Của Hàm Số

Dạng toán này yêu cầu học sinh tính giới hạn của các hàm số mũ và logarit khi biến số tiến dần về một giá trị nhất định. Việc nắm vững các công thức tính giới hạn đặc biệt là điều kiện tiên quyết để giải quyết các bài tập dạng này.

e. Dạng 5: Tìm GTLN, GTNN Trên Một Đoạn

Dạng toán này yêu cầu học sinh tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số mũ và logarit trên một đoạn nhất định.

Kết Luận

Bài viết đã cung cấp toàn bộ kiến thức cơ bản và bài tập liên quan đến hàm số mũ và hàm số logarit. Hy vọng rằng các em học sinh sẽ nắm vững những kiến thức này để chuẩn bị tốt nhất cho kỳ thi quan trọng sắp tới. Hãy kiên trì ôn luyện và không ngừng cố gắng!