Vectơ là một phần quan trọng trong toán học và được ứng dụng rộng rãi trong nhiều lĩnh vực thực tế. Học tốt các công thức tính Vectơ giúp bạn phát triển kỹ năng phân tích và giải quyết các bài toán phức tạp. Hãy cùng khám phá chi tiết về lý thuyết và bài tập ứng dụng liên quan đến Vectơ trong chương trình lớp 10.
Lý Thuyết Tổng Hợp Về Vectơ
Vectơ không chỉ là một khái niệm cơ bản trong toán học mà còn đóng vai trò nền tảng trong nhiều bài toán thực tế. Hiểu rõ về lý thuyết Vectơ giúp bạn phát triển tư duy logic và không gian, từ đó nâng cao khả năng giải toán.
Định Nghĩa Vectơ
Vectơ là một đoạn thẳng có hướng, có điểm đầu và điểm cuối. Chúng thường được sử dụng để biểu diễn các đại lượng có cả độ lớn và hướng như lực, vận tốc hay gia tốc. Một Vectơ trong không gian hai chiều có thể được biểu diễn bằng tọa độ như sau: A=(a₁, a₂). Trong không gian ba chiều, Vectơ có dạng: A=(a₁, a₂, a₃).
Vectơ Cùng Phương và Cùng Hướng
Hai Vectơ được gọi là cùng phương khi chúng có giá song song hoặc trùng nhau. Điều này không nhất thiết yêu cầu chúng có cùng độ lớn hoặc hướng. Trong khi đó, hai Vectơ cùng hướng không chỉ cùng phương mà còn cùng chiều. Điều kiện để hai Vectơ cùng hướng là chúng phải thỏa mãn: B = kA với k > 0.
Vectơ Bằng Nhau
Hai Vectơ bằng nhau nếu chúng có cùng độ lớn và hướng. Điều này có nghĩa là khi di chuyển một Vectơ mà không thay đổi độ dài và hướng, nó sẽ bằng với Vectơ ban đầu. Đây là khái niệm quan trọng khi giải quyết các bài toán so sánh đại lượng.
Vectơ – Không
Vectơ – không là một Vectơ có tọa độ là 0 trong tất cả các chiều và đóng vai trò trung tính trong phép cộng Vectơ. Nó được ký hiệu là 0 = (0, 0, 0) trong không gian ba chiều.

Phép Toán Cơ Bản Với Vectơ
Cùng với các định nghĩa cơ bản, chúng ta cần nắm vững các phép toán cơ bản của Vectơ như phép cộng, hiệu và tích với một số.
Tổng Và Hiệu Của Hai Vectơ
Phép cộng Vectơ là phép toán cơ bản giúp ta tìm tổng của hai Vectơ. Tính chất của phép cộng này được biểu diễn theo quy tắc hình bình hành. Hiệu của hai Vectơ là kết quả của phép trừ các thành phần tương ứng. Nếu hai Vectơ là A = (a₁, a₂) và B = (b₁, b₂), thì tổng của chúng là: A + B = (a₁ + b₁, a₂ + b₂) và hiệu là A − B = (a₁ − b₁, a₂ − b₂).
Tích Của Vectơ Với Một Số
Tích của một Vectơ với một số thực k được tính bằng cách nhân mỗi thành phần của Vectơ với số đó. Ví dụ, nếu A = (a₁, a₂) thì tích của A với k là kA = (ka₁, ka₂).
Hệ Trục Tọa Độ
Hệ trục tọa độ là nền tảng để xác định vị trí của các điểm trong không gian và đóng vai trò quan trọng trong các bài toán về Vectơ. Hệ trục Descartes bao gồm hai trục chính: trục hoành (trục x) và trục tung (trục y), vuông góc với nhau. Trong không gian ba chiều, chúng ta có thêm trục z.
Tọa Độ Của Một Vectơ
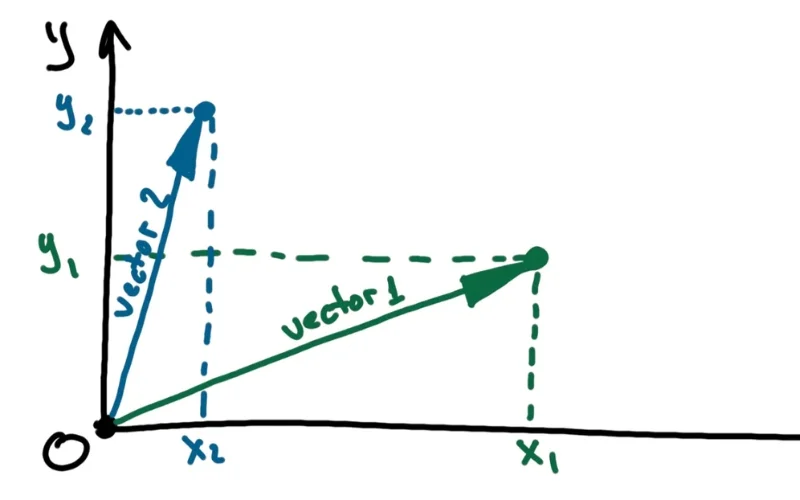
Tọa độ của một Vectơ là các giá trị xác định hướng và độ lớn của nó. Ví dụ, nếu A là Vectơ có điểm đầu tại (x₁, y₁) và điểm cuối tại (x₂, y₂), thì tọa độ của A là (x₂ – x₁, y₂ – y₁).
Tọa Độ Trung Điểm Và Trọng Tâm
Trung điểm của đoạn thẳng nối hai điểm A(x₁, y₁) và B(x₂, y₂) được xác định bằng công thức: M = [(x₁ + x₂)/2, (y₁ + y₂)/2]. Trọng tâm của một tam giác có các đỉnh A(x₁, y₁), B(x₂, y₂), và C(x₃, y₃) được tính bằng: G = [(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3].
Bài Tập Ứng Dụng Vectơ
Để hiểu rõ hơn về Vectơ, việc luyện tập với các bài toán cụ thể là rất cần thiết. Dưới đây là một số dạng bài tập phổ biến với các công thức tính Vectơ, kèm theo lời giải.
Bài Tập 1: Tìm Tọa Độ Của Một Điểm
Cho ba điểm A(1, 2, 3), B(4, 6, 8) và C(7, 9, 11). Yêu cầu tìm tọa độ điểm D chia đoạn BC theo tỷ lệ 2:3 và tính Vectơ AD.
Lời giải:
- Tọa độ của điểm D được tính bằng công thức điểm chia đoạn thẳng theo tỷ lệ.
- Sau khi tìm được tọa độ D, ta áp dụng công thức tọa độ Vectơ để tính Vectơ AD.
Bài Tập 2: Tìm Tổng Của Hai Vectơ
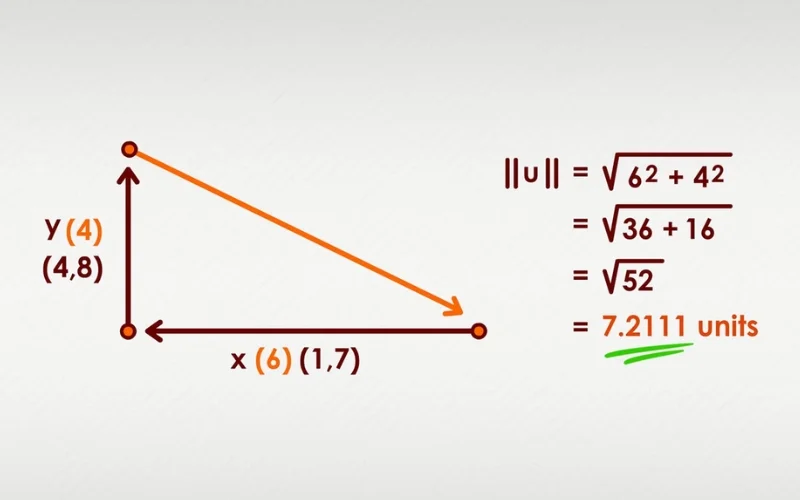
Cho hai Vectơ u = (2, −1, 3) và v = (−4, 5, 1). Tính tổng của u và v, đồng thời tính tổng của nhiều Vectơ.
Lời giải:
- Tổng của hai Vectơ được tính bằng cách cộng từng thành phần tương ứng của chúng.
- Nếu có nhiều Vectơ, ta cộng tất cả các thành phần của chúng lại với nhau.
Bài Tập 3: Phân Tích Một Vectơ Qua Hai Vectơ Không Cùng Phương
Cho Vectơ v = (7, 8) và hai Vectơ không cùng phương u = (1, 2) và w = (3, 1). Phân tích Vectơ v theo u và w.
Lời giải:
- Phương trình v = au + bw sẽ dẫn đến một hệ phương trình hai ẩn. Giải hệ này, ta tìm được các hệ số a và b.
Kết Luận
Những kiến thức và bài tập liên quan đến công thức Vectơ là một phần quan trọng trong chương trình Toán học lớp 10. Chúng không chỉ giúp phát triển tư duy mà còn là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai. Trường Việt Anh hy vọng rằng, thông qua bài viết này, bạn sẽ nắm vững kiến thức về Vectơ và có thể áp dụng vào học tập và thi cử một cách hiệu quả.
